如何通俗易懂地解释卷积？

  卷积这个概念，很早以前就学过，但是始终没搞懂。教科书上通常会给出定义，给出很多性质，也会用实例和图形进行解释，但究竟为何需要这么设计，这么计算，背后的意义是什么，往往语焉不详。作为一个学物理出身的人，一个公式倘若倘若给不出结合实际的直观的通俗的解释（也就是背后的“物理”意义），就觉得少了点什么，觉得不是真的懂了。

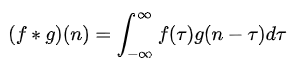
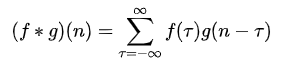
  并且也解释了，先对g函数进行翻转，相当于在数轴上把g函数从右边褶到左边去，也就是卷积的“卷”的由来。

  然后再把g函数平移到n，在这一个位置对两个函数的对应点相乘，然后相加，这样的一个过程是卷积的“积”的过程。

  这个只是从计算的方式上对公式进行了解释，从数学上讲无可挑剔，但进一步追问，为何需要先翻转再平移，这么设计有何用意？还是有点费解。

  在知乎，已经很多的热心网友对卷积举了很多形象的例子进行了解释，如卷地毯、丢骰子、打耳光、存钱等等。读完觉得非常生动有趣，但过细想想，还是感觉有些地方还是没解释清楚，甚至有可能还有瑕疵，或者还可以改进（这些后面我会做一些分析）。

  带着问题想了两个晚上，终于觉得有些问题想通了，所以就写出来跟网友分享，一同学习提高。不对的地方欢迎评论拍砖。。。

  一个输入信号f(t)，经过一个线性系统（其特征可以用单位冲击响应函数g(t)描述）以后，输出信号应该是什么？实际上通过卷积运算就能够获得输出信号。

  输入一幅图像f(x,y)，经过特定设计的卷积核g(x,y)进行卷积处理以后，输出图像将会得到模糊，边缘强化等各种效果。

  对卷积这个名词的理解：所谓两个函数的卷积，本质上是先将一个函数翻转，接着进行滑动叠加。

  在连续情况下，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和，为简单起见就统一称为叠加。

  翻转——>

  滑动——>

  叠加——>

  滑动——>

  叠加——>

  滑动——>

  叠加.....

  卷积的“卷”，指的的函数的翻转，从 g(t) 变成 g(-t) 的这个过程；同时，“卷”还有滑动的意味在里面（吸取了网友李文清的建议）。如果把卷积翻译为“褶积”，那么这个“褶”字就只有翻转的含义了。

  有些文章只强调滑动叠加求和，而没有说函数的翻转，我觉得是不全面的；有的文章对“卷”的理解其实是“积”，我觉得是张冠李戴。

  1. 从“积”的过程能够正常的看到，我们得到的叠加值，是个全局的概念。以信号分析为例，卷积的结果是不仅跟当前时刻输入信号的响应值有关，也跟过去所有时刻输入信号的响应都有关系，考虑了对过去的所有输入的效果的累积。在图像处理的中，卷积处理的结果，实际上的意思就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或是说一种“混合”，把两个函数在时间或者空间上进行混合。

  2. 那为何需要进行“卷”？直接相乘不好吗？我的理解，进行“卷”（翻转）的目的其实是施加一种约束，它指定了在“积”的时候以什么为参照。在信号分析的场景，它指定了在哪个特定时间点的前后进行“积”，在空间分析的场景，它指定了在哪个位置的周边进行累积处理。

  如下图所示，输入信号是 f(t) ，是随时间变化的。系统响应函数是 g(t) ，图中的响应函数是随时间指数下降的，它的物理意义是说：如果在 t=0 的时刻有一个输入，那么跟着时间的流逝，这个输入将不断衰减。换言之，到了 t=T时刻，原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。

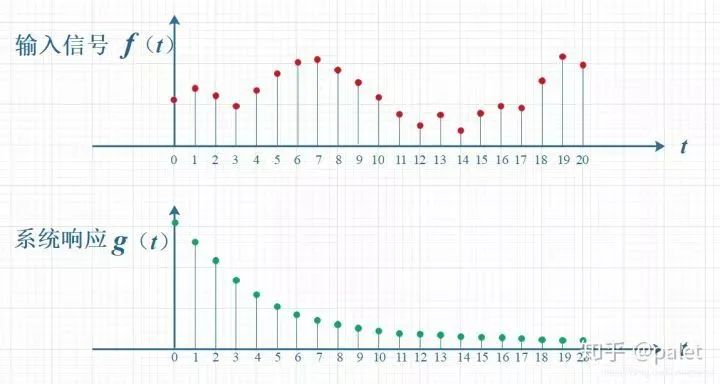
  考虑到信号是连续输入的，也就是说，每个时刻都有新的信号进来，所以，最终输出的是所有之前输入信号的累积效果。如下图所示，在T=10时刻，输出结果跟图中带标记的区域整体有关。其中，f(10)因为是刚输入的，所以其输出结果应该是f(10)g(0)，而时刻t=9的输入f(9)，只经过了1个时间单位的衰减，所以产生的输出应该是 f(9)g(1)，如此类推，即图中虚线所描述的关系。这些对应点相乘然后累加，就是T=10时刻的输出信号值，这个结果也是f和g两个函数在T=10时刻的卷积值。

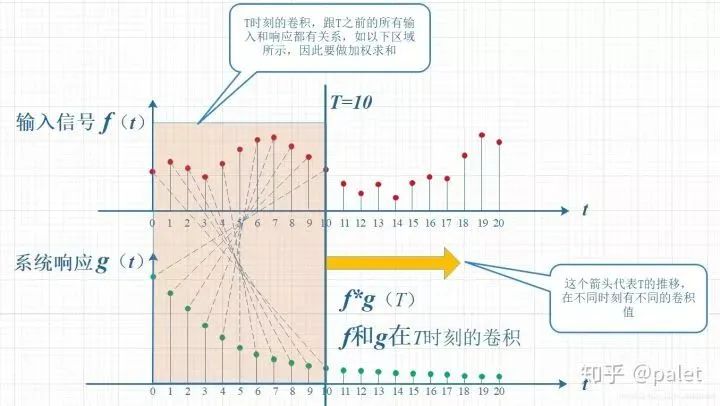
  显然，上面的对应关系看上去比较难看，是拧着的，所以，我们把g函数对折一下，变成了g(-t)，这样就好看一些了。看到了吗？这就是为什么卷积要“卷”，要翻转的原因，这是从它的物理意义中给出的。

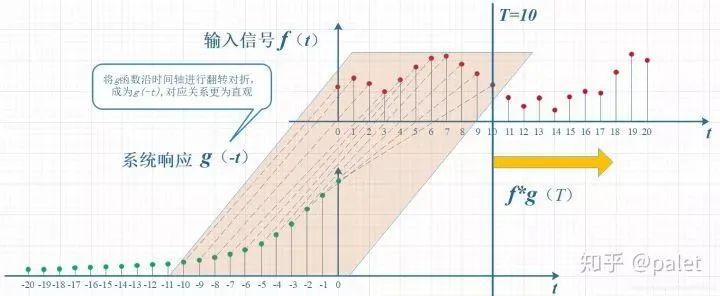
  上图虽然没有拧着，已经顺过来了，但看上去还有点错位，所以再进一步平移T个单位，就是下图。它就是本文开始给出的卷积定义的一种图形的表述：

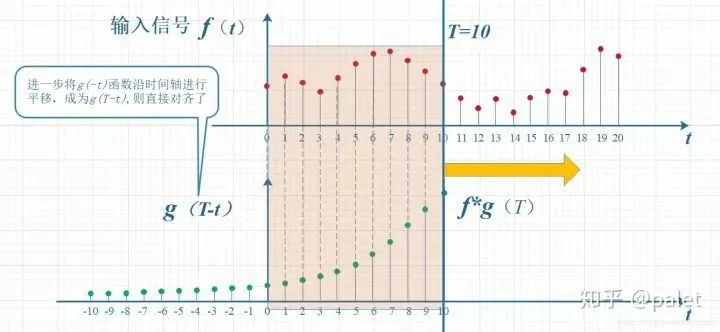
  所以，在以上计算T时刻的卷积时，要维持的约束就是：t+ (T-t) = T  。这种约束的意义，你们可以自己体会。

  在本问题 如何通俗易懂地解释卷积？中排名第一的马同学在中举了一个很好的例子（下面的一些图摘自马同学的文章，在此表示感谢），用丢骰子说明了卷积的应用。

  要解决的问题是：有两枚骰子，把它们都抛出去，两枚骰子点数加起来为4的概率是多少?

  分析一下，两枚骰子点数加起来为4的情况有三种情况：1+3=4， 2+2=4, 3+1=4

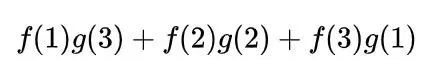
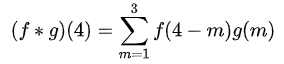
  首先，因为两个骰子的点数和是4，为满足这个约束条件，我们仍旧是把函数 g 翻转一下，然后阴影区域上下对应的数相乘，然后累加，相当于求自变量为4的卷积值，如下图所示：

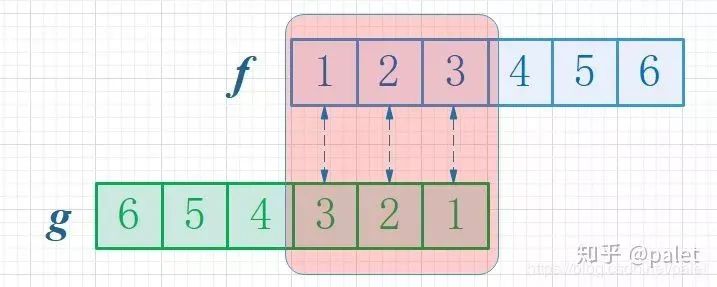
  进一步，如此翻转以后，可以方便地进行推广去求两个骰子点数和为 n 时的概率，为f 和 g的卷积 f*g(n)，如下图所示：

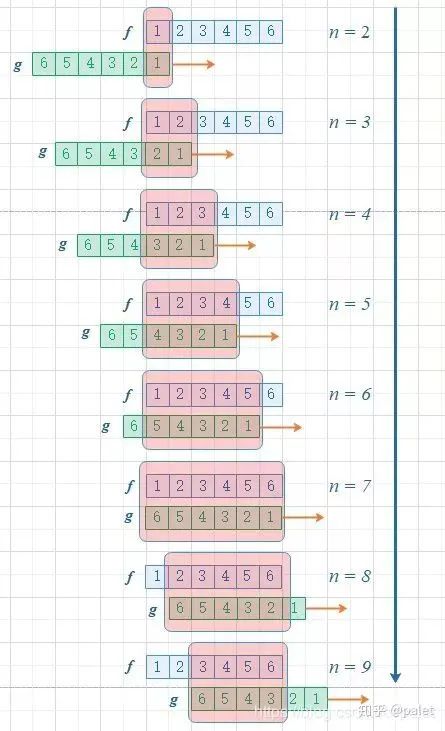
  由上图能够正常的看到，函数 g 的滑动，带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和，它也是卷积函数的自变量。有兴趣还可以算算，如果骰子的每个点数出现的概率是均等的，那么两个骰子的点数和n=7的时候，概率最大。

  还是引用知乎问题 如何通俗易懂地解释卷积？中马同学的例子。图像可以表示为矩阵形式（下图摘自马同学的文章）：

  对图像的处理函数（如平滑，或者边缘提取），也可以用一个g矩阵来表示，如：

  然后将图像处理矩阵翻转（这个翻转有点意思，不是延x轴和y轴两个方向翻转，而是沿右上到左下的对角线翻转，这是为了凑后面的内积公式。），如下：

  请注意，以上公式有一个特点，做乘法的两个对应变量a,b的下标之和都是（u,v），其目的是对这种加权求和进行一种约束。这也是怎么回事要将矩阵g进行翻转的原因。以上矩阵下标之所以那么写，并且进行了翻转，是为了让大家更清楚地看到跟卷积的关系。这样做的好处是便于推广，也便于理解其物理意义。实际在计算的时候，都是用翻转以后的矩阵，直接求矩阵内积就可以了。

  以上计算的是（u,v）处的卷积，延x轴或者y轴滑动，就可以求出图像中各个位置的卷积，其输出结果是处理以后的图像（即经过平滑、边缘提取等各种处理的图像）。

  再深入思考一下，在算图像卷积的时候，我们是直接在原始图像矩阵中取了（u,v）处的矩阵，为何需要取这个位置的矩阵，本质上其实是为满足以上的约束。因我们要算（u，v）处的卷积，而g矩阵是3x3的矩阵，要满足下标跟这个3x3矩阵的和是（u,v），只能是取原始图像中以（u，v）为中心的这个3x3矩阵，即图中的阴影区域的矩阵。

  推而广之，如果如果g矩阵不是3x3，而是6x6，那我们要在原始图像中取以（u，v）为中心的6x6矩阵进行计算。由此可见，这种卷积就是把原始图像中的相邻像素都考虑进来，进行混合。相邻的区域范围取决于g矩阵的维度，维度越大，涉及的周边像素越多。而矩阵的设计，则决定了这种混合输出的图像跟原始图像比，究竟是模糊了，还是更锐利了。

  比如说，如下图像处理矩阵将使得图像变得更加平滑，显得更模糊，因为它联合周边像素进行了平均处理：

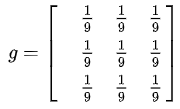
  而如下图像处理矩阵将使得像素值变化明显的地方更明显，强化边缘，而变化平缓的地方没有影响，达到提取边缘的目的：

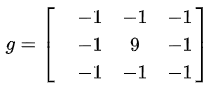
  上面一些对卷积的形象解释，如知乎问题 卷积为什么叫「卷」积？中荆哲以及问题 如何通俗易懂地解释卷积？中马同学等人提出的如下比喻：

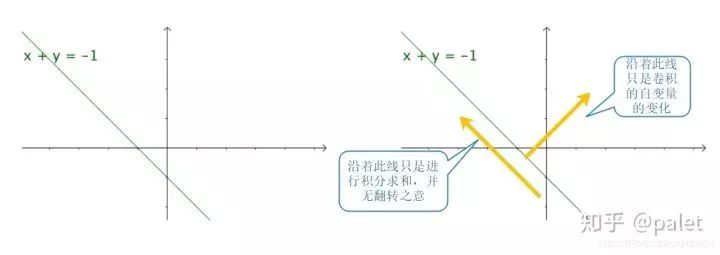
  其实图中“卷”的方向，是沿该方向进行积分求和的方向，并无翻转之意。因此，这种解释，并没有完整描述卷积的含义，对“卷”的理解值得商榷。

  声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。举报投诉

  Wi-Fi被普遍误以为是指无线保真(Wireless Fidelity) 。但事实上, Wi-Fi- -词没有一点意义,也没有全称。它只是模仿了音频领域Hi-Fi (High- -Fidelity, 高保线

  傅里叶变换（Fourier Transform，简称FFT）是一个大范围的应用的数学工具，它可以将一个连续或离散信号分解成一系列单一的正弦函数，这些正弦函数名称为频率成分或

  。CNN能够在一定程度上帮助人们实现许多有趣的任务，如图像分类、物体检测、语音识别、自然语言处理和视频分析等。本文将详细介绍

  神经网络是一个由神经元构成的深度神经网络，由输入层、隐藏层和输出层组成。在

  操作是一种数学上的操作，它可以将两个函数f和生第三个函数h。在机器

  FPGA和ASIC的概念、基本组成及其应用场景 FPGA与ASIC的比较

  FPGA和ASIC都是数字电路的实现方式，但它们有不同的优缺点和应用场景。本文将以

  上图所示的是电脑显示屏的微观图像，拍摄的方法非常有意思，通过在手机摄像头上滴一滴水滴，形成凸透镜，就能做成一个简易版的显微镜。

  收集NLP各种任务的数据集，加上任务描述和提示组装成新的数据集，并使用这一些数据微调预训练的大型语言模型。包括指令微调和有监督微调。

  离开无线，就无所谓射频。 我们今天所说的Radio Frequency RF就是指电磁波中这段能用来无线通信的电磁波频谱。 无线信号能够以电磁波为载体进行传输，就像光线一样，脱离实物载体，实现无线传输，唯一不同的是频率和波长。

  所以，在大多数场合中，用“开关量”来控制一个物理量，就显得最简单粗暴了。有时候，是无法保持稳定的。因为单片机、传感器不是无限快的，采集、控制需要时间。

  ：带串口控制的液晶屏，故串口+屏，可组态方式二次开发的智能串口控制显示屏，是指带有串口通信的TFT彩色液晶屏显示控制模组。

  BGP是自治系统间的路由协议，BGP交换的网络可达性信息提供了足够的信息来检测路由回路并根据性能优先和策略约束对路由进行决策。

  抛开所有和人工智能(AI)有关的扯淡成分，机器学习唯一的目标是基于输入的数据来预测结果，就这样。所有的机器学习任务都可以用这种方式来表示，否则从一开始它就不是个机器学习问题。

  的语句介绍LC光纤快速连接器”由德索连接器为您编辑整理，采购连接器，上德索。光纤快速连接器是一种灵活的设备，能够迅速连接和断开光纤电缆。有多种类型的光纤快速连接器可以再一次进行选择，包括LC光纤

  的电脑电源选购知识指南一、电源品牌电源品牌众多，例如海盗船、安钛克、全汉、台达、振华、酷...

  Modbus是一种工业协议，于1979年开发，旨在实现自动化设备之间的通信。本章采用

  Modbus的通信原理，最重要的包含Modbus-RTU协议以及Modbus-ASCLL协议。

  学过电力电子的小伙伴们都知道…交流电“整流”为直流电（a）…直流电“逆变”为交流电（b）…交流电“变压”为交流电（c）…直流电“斩波”为直流电（d）…“变压”（c）暂且不谈…这是变压器制...

  ！资料下载的电子资料下载，更有其他相关的电路图、源代码、课件教程、中文资料、英文资料、参考设计、用户指南、解决方案等资料，希望有机会能够帮助到广大的电子工程师们。

  ，看完你也会啊！资料下载的电子资料下载，更有其他相关的电路图、源代码、课件教程、中文资料、英文资料、参考设计、用户指南、解决方案等资料，希望能够在一定程度上帮助到广大的电子工程师们。

  ！资料下载的电子资料下载，更有其他相关的电路图、源代码、课件教程、中文资料、英文资料、参考设计、用户指南、解决方案等资料，希望有机会能够帮助到广大的电子工程师们。

  01 工厂方法 追 MM 少不了请吃饭了，麦当劳的鸡翅和肯德基的鸡翅都是 MM 爱吃的东西，虽然口味不一样，但不管你带 MM 去麦当劳或肯德基，只管向服务员说「来四个鸡翅」就行了。麦当劳和肯德基就是生产鸡翅的 Factory 工厂模式：客户类和工厂类分开。 消费者任何一个时间里需要某种产品，只需向工厂请求即可。消费者无须修改就可以接纳新产品。缺点是当产品修改时，工厂类也要做相应的修改。如：如何创建及如何向客户端提供。 02 建造者模式 MM 最爱

  的传播，设身处地以用户思维进行优质的内容生产，从而打造具有影响力、契合新媒体传播语境的爆款作品，一直是传统主流媒体展示媒体融合创新成果的重要舞台。

  ，似乎默认所有读者都有相关基础。这篇外文既友好又深入，所以翻译了过来。文章高级部分通过流体力学量子力学等

  相信网上现在有很多关于FFT的教程，我曾经也参阅了很多网上的教程，感觉都不怎么

  机器学习基本概念时最有启发性的条目列表。 1. Test and training error: 为什么低训练误差并不总是一件好的事情呢：以模型复杂度为变量的测试及训练错误

  贝叶斯网络和它的应用？详情请看下文。贝叶斯网络是一个用严格的数学方法来模拟一个世界的方法，是灵活的，适应于任何你拥有的知识程度的方法，同时也是计算效率的方法。

  场效应管具有输入电阻高（107～1015Ω）、噪声小、功耗低、动态范围大、易于集成、没有二次击穿现象、安全工作区域宽等优点，现在已经成为双极型晶体管和功率晶体管的强大竞争者。用

  区块链如何运作的? 下面这篇文翻译自How Does the Blockchain Work?全文。作者Michele DAliessi用

  ) · 导语 2010年，您是否有购买笔记本的计划？作为一款对多数人来说都价格不

  的《路由和交换》 路由和交换是网络世界中两个重要的概念。传统的交换发生在网络的第二层，即数据链路层，而路由则发